製造系統管理第九章預習重點(4)
以下Q代表Question、T代表Translation、A代表Answer、E代表Explanation
Q：Given the following chart and equations, answer the following questions.
Time
at the first station
Show
the equation for the average time before batching.
Show
the equation for the average wait-to-batch time.
Show
the equation for the average time spent at the first station
Show
the equation for the output of First Station.
Show
the equation for the SCV of batch arrivals to station 2.
 |
| Move Batching Problem |
 |
| The given equation |
T&
A：
給予下列圖與方程式，回答下列問題
寫出在批量處理前的平均時間。P.S.此處不會包含進入機台的加工時間
Sol：
在第一個工作站前的排隊等待時間，即為本題所求。利用CTq=VUT公式求解。
第一站的到達CV等於Ca(1)，加工的CV等於Ce(1)，利用率則以u=ra te/m求出，此處te=t(1)。
 |
| Average time before batching |
寫出平均等待批量集結的方程式。
 |
| Average wait-to-batch time |
(解釋)
首件工件，在加工完成後，需要花費時間等待其他k-1件的抵達，也就是
第二件工件，在加工完成後，需要花費時間等待其他k-2件的抵達，也就是
末件工件則無需等待，故為等待時間為0。
總等待時間為一首項為(k-1)/ra，末項為0，共有k項的等差數例，故等差級數(等差數列之和)=
等差級數平均至每一項工件(共有k件)的等待，即可求出解答，又因為u(1)=ra*te(1)，可以將ra替換成利用率與實際加工時間。
寫出在第一站平均花費時間的方程式
 |
| Average time spent at the first station |
(解釋)此方程式的加總的項目分別為批量處理前等待時間加上實際加工時間和平均等待批量集結時間。
第一站的輸出方程式。
Sol：題意的部分並沒有說明輸出是指產出速率或其他先前學過的指標。因此本題會根據講義直接以單件/整批產出間隔時間做為說明。
Time
between output of individual parts into the batch is ta.
Time
between output of batches of size k is k ta.
Variance
of interoutput times of parts is
Variance of
interoutput times of batches of size k is
寫出批量抵達第二工作站的SCV方程式
Sol：其SCV可用該批量的間隔產出時間變異除以間隔產出時間的平方，過程如下式：
Time at Second Station
Show the equation for the time to process a batch of size k.
Show the equation for the variance of time to process a batch of size k.
Show the equation for the SCV for a batch of size k.
Show the equation for the mean time spent in partial batch of size k.
Show the equation for the average time spent at the second station.
Show the equation for the total cycle time (including both stations 1
and 2.
What is the managerial insight from the following equation?
T
& A：
加工一個批量大小為k所需要花的時間
Sol：批量大小為k，即有k個工件，加工k個工件的時間就是直觀的kt(2)
加工一個批量大小為k的時間的變異
Sol：批量大小為k，即有k個工件。根據題目所給定的圖，我們可以用加工時間的平均數與SCV，求出變異。
 |
| SCV definition |
 |
| Original variance at station 2 |
而每一個工件加工時間為獨立，則其變異也為k倍，
一個批量大小為k的SCV
Sol：根據上一題所求出的變異，除以k件的平均加工時間平方，如下所示：
平均花在一批量大小為K的時間P.S.此處不會包含進入機台的加工時間
Sol：
首件工件，可直接進入工作站進行加工，因此等待時間為0。
第二件工件，則需等待首件加工完成後，才能進入工作站進行加工，因此需要花費時間等待其他1件的抵達，也就是t(2)。
第k件工件，則需等待前面(k-1)件加工完成後，才能進入工作站進行加工，因此所需要花費等待時間為(k-1)t(2)。
總等待時間為一首項為0，末項為(k-1)t(2)，共有k項的等差數例，故等差級數(等差數列之和)=k(k-1)t(2)/2
等差級數平均至每一項工件(共有k件)的等待，即可求出=(k-1)t(2)/2
平均在第二工作站花費時間
Sol：
 |
| CT at Station2 |
總週期時間(包含工作站1和2)
其中
故可以改寫成
Q：從以下的方程式我們可以得到什麼管理上的意義
A：
A：
CT會隨著批量大小k值的增加而增加
批量變動的影響不包含CV
批量造成的壅塞比隨機性還嚴重
Q：Explain the following cycle time components.( Wait-to-batch time、Wait-in-batch time、Wait-to-match time)
T：解釋以下CT組成的元件：(等待形成批量的時間、在批量狀態下等待的時間、等待組合的時間)
A：
Wait-to-batch time：在形成批量所花費的時間，因為形成批量才可以加工或移動。
Wait-in-batch time：整個批量已經到達工作站，但工作站只能一個一個做，其他工件皆屬於等待的狀態。
Wait-to-match time：需要多種零件皆到達才能進行加工，會有等待組裝的時間。
Q：Why is cycle time a random variable?
T：為何週期時間是一個隨機變數?
A：單一工件在走完加工流程所需花費的時間為週期時間，然而工作站的加工時間存在變異，因此，週期時間是一個隨機變數。
Q：Why is lead time a constant?
T：為何前置時間是一個常數?
A：前置時間指的是我們期待的或是最大允許的週期時間，由於是像顧客承諾或與顧客議定的，因此為一常數。
Q：What is the difference between customer lead
time and manufacturing lead time?
T：顧客前置時間與製造前置時間之間有什麼不同?
A：顧客前置時間則為與顧客議定的、工廠與顧客承諾的。製造的前置時間則是在特定的途程下加工的花費的時間。通常manufacturing lead time
< customer lead time，才可準時交貨。
Q：What is the difference between service level
and fill rate?
T：服務水準與完成率之間有什麼不同?
A：兩者適用的生產型態不同，服務水準用於MTO的生產型態，代表在承諾的前置時間內完成的比例。完成率用於MTS的生產型態。
Q：What is the managerial insight from the
following chart?
T：從下圖中我們可以得到什麼管理意涵?
A：承諾水準(交期)是以CT+zs*(CT的標準差)來訂出，在圖中為了要達到95%服務水準，在週期時間平均數相同的情況下，CT變異大者的需要較長前置時間，才能達成預定的服務水準。
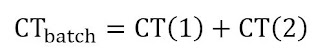
留言
張貼留言